GEOMETRIA 5-PRE-2021S

Por la medida de sus elementos - Polígono Equiángulo: Cuando los ángulos interiores y exteriores son de la misma medida. x

POLÍGONOS 

B 

 



x C

 

 

 x



   D

A   

  E



x

x



- Polígono Equilátero: Cuando los lados tienen igual longitud. B

Notación: Polígono ABCDE Vértices: A, B, C, D, E Lados: AB, BC, CD, DE, EA Ángulos Internos: , , , ,  Ángulos Externos: , , , ,  Diagonales: AC, BD, …

A

C

E

CLASIFICACIÓN Por la región que limitan - Polígono Convexo: cuyos ángulos interiores son menores de 180º. D C E B

F

A



D

- Polígono Regular: Cuando los ángulos y lados tienen la misma medida. C  B

 

A





O 

D

E

Donde: “O” es el centro del polígono.

G

- Polígono No convexo (cóncavo): cuando uno o más ángulos son mayores de 180º. D

NOMENCLATURA POR LA CANTIDAD DE LADOS - Polígono de 3 lados: __________________ - Polígono de 4 lados: __________________

B

- Polígono de 5 lados: __________________ C A

F

E

- Polígono de 6 lados: __________________ - Polígono de 7 lados: __________________ - Polígono de 8 lados: __________________

1

- Polígono de 9 lados: __________________ - Polígono de 10 lados: _________________

EJERCICIOS PARA LA CLASE 1.

Calcule la suma de medidas de los ángulos exteriores de un octógono. A) 360º B) 420º C) 720º D) 540º E) 600º

2.

Según el gráfico, ABCDEF es un hexágono regular. Calcule .

- Polígono de 11 lados: _________________ - Polígono de 12 lados: _________________ - Polígono de 15 lados: _________________ - Polígono de 20 lados: _________________ PROPIEDADES Relación de lados, vértices, ángulo Nº vértices = Nº lados = Nº ángulos = n Suma de medidas de los ángulos internos (Si) Si = 180 (n - 2) Suma de medidas de los ángulos externos (Se) Se = 360º

3.



A) 75º D) 56º 4.

Número de diagonales desde un vértice ND  n  3

B) 80º E) 52º

E

5.

B

A C) 64º

En el gráfico, ABCDEF es un hexágono regular y AB = 3. Calcule FC. B C A) 9 B) 12 C) 8 A D D) 5 E) 6 F

1v

D

Del gráfico, ABCD y DEA son polígonos

D

Suma de un ángulo interior y un ángulo exterior ∡i + ∡e = 180º

Número total de diagonales n(n  3) ND  2

A

regulares. Calcule m∢EBA. C E

Medida de un ángulo externo en polígonos equiángulos (∡e) 360 ∡e = n

Número de diagonales desde “k” vértices consecutivos (k  1)(k  2) ND  nk  kv 2

C

F

Medida de un ángulo interno en polígonos equiángulos (∡i) 180(n  2) ∡i = n

NOTA: Solo en polígono regular Ángulo central = ángulo exterior ∡c =∡e

B

A) 30º B) 60º C) 45º D) 53º E) 75º

E

Indique el valor de los siguientes enunciados. I. El triángulo tiene 3 diagonales. II. El cuadrilátero tiene 2 diagonales. III. Al polígono de 5 lados se le denomina pentágono. A) FVV B) FFV C) FFF D) VVV E) VVF

2

6.

En el gráfico, ABCDE es un pentágono regular. Calcule . B A) 56º B) 37º C) 60º D) 74º E) 45º

PROBLEMAS PROPUESTOS 1.

D

Del gráfico, ABCDEF es un hexágono regular y AE = 2. Calcule CG. A) 1,41 B) 1,73 C) 1 D) 1,5 E) 0,71

Rpta.: ____________

C



E 7.

Calcular m∢CMD

84°

A

13. Se tiene el polígono regular ABCDEFGH, exteriormente al lado DE, se construye el polígono regular DMNPQF.

B

C

Rpta.: ____________ 2.

¿Qué polígono tiene 44 diagonales? Rpta.: ____________

A

D

3.

F

Hallar la suma de ángulos internos de aquel polígono que tiene 14 diagonales. Rpta.: ____________

G

8.

¿En qué polígono la suma de ángulos internos es 1260?

E

Hallar la suma de ángulos internos del polígono que tiene 54 diagonales. a) 1260º b) 1080º c) 900º d) 1440º e) 1620º

4.

¿En qué polígono regular su ángulo interno es el triple de su ángulo central? Rpta.: ____________

5.

Calcular el número de vértices de un polígono cuyo número de diagonales es igual al triple del número de lados. a) 10 b) 11 c) 12 d) 9 e) 8

Calcule el número de diagonales de un pentágono. A) 2 B) 6 C) 3 D) 4 E) 5

6.

10. Si en un polígono se duplica su número de lados, su número de diagonales aumenta en 18. Calcular su número de lados. a) 8 b) 6 c) 4 d) 5 e) 3

En un polígono el número de diagonales es igual a seis veces el número de lados. Hallar dicho número de lados. a) 14 b) 12 c) 18 d) 15 e) 20

7.

11. Si la relación entre el ángulo interior y exterior de un polígono regular es de 7 a 2. Hallar el número total de sus diagonales. a) 27 b) 20 c) 35 d) 44 e) 56

En un polígono la suma de las medidas de los ángulos internos y externos es 2520°. Calcular el número de lados del polígono. a) 8 b) 14 c) 12 d) 10 e) 20

8.

En un polígono regular el número de diagonales aumentado en el número de vértices es igual a 153. Calcular el valor de su ángulo central. a) 20° b) 18° c) 36° d) 45° e) 30°

9.

12. Hallar el número de diagonales del polígono regular cuyo ángulo exterior mide 24°. Rpta.: ____________

3

9.

Si en un polígono se aumenta un lado su número de diagonales aumenta en seis. Calcular su número de lados. a) 6 b) 7 c) 8 d) 10 e) 12

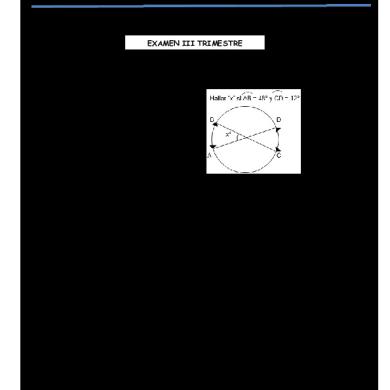
13. Si los polígonos son regulares, hallar “x°”

10. A partir del gráfico, calcule la suma de medidas de los ángulos interiores. xº a) 10° d) 24° A) 720º D) 840º

B) 900º E) 590º

C) 660º

11. Según el gráfico, calcule x. x

x

c) 20°

14. Si los polígonos son regulares hallar “x°” a) b) c) d) e)

x

b) 15° e) 30°

10° 15° 20° 24° 30° xº

x A) 72º D) 60º

B) 105º E) 81º

C) 90º

12. A partir del gráfico, calcule .  

A) 127º D) 108º

16. En un polígono convexo desde 4 vértices consecutivos se pueden trazar como máximo 65 diagonales, hallar la suma de los





∢s internos de dicho polígono. a) 3240° b) 7200° c) 2340° d) 3000° e) 2440°

 B) 120º E) 153º

15. En un hexágono regular ABCDEF. Calcular el ángulo FBD. a) 40° b) 60° c) 45° d) 37° e) 30°

C) 100º

4