Tarea 2 Robert Collazos

Tarea 2 – Reconocer los elementos matemáticos que implica la conversión Analógica Digital

Tutor: Mauricio Alberto García

Estudiante: Robert Santiago Collazos Bonilla Cod. 1110589404

Estudiante de Ingeniería Electrónica

Grupo: 2150504-36

Universidad Nacional Abierta y a Distancia UNAD Sistemas de Comunicación CEAD Ibagué -Tolima 2021

Primera parte.

1) ¿A qué se refiere el muestreo de una señal analógica? Es la toma de información de una señal cada tiempo predeterminado, programado descuerdo a las necesidades y a la cantidad de datos que se quieren analizar dentro de la señal. 2) ¿Cómo se realiza la cuantización de una señal? la cuantización se debe de hacer teniendo en cuenta la amplitud de la señal, es decir la resolución dada en dB, nos dictamina la cantidad de niveles que vamos realizarle a la seña. L=2 dB

3) ¿Qué indica el teorema de muestreo de Nyquist? Dado que se toma una frecuencia y se le dictamine un muestreo, donde este mismo determine una lectura de la señal, posteriormente se reconstruya esta señal en base al muestreo realizado, para que este muestreo tenga una buena lectura y su reconstrucción sea los más similar a la original se debe tener en cuenta el teorema, donde dictamina que la frecuencia de muestreo sea el doble o más de la máxima frecuencia que tenga la señal original. f s ≥2 fmax

4) ¿Cuál es el fenómeno llamado Alias o Aliasing? Este efecto se lleva a cabo cuando no se tiene en cuenta el teorema de muestreo de Nyquist, dado que el muestreo es sumamente precario y esto crea una señal de baja frecuencia cuando se hace la reconstrucción, originando una pérdida de información dado que el muestreo es insuficiente, para reproducir una señal parecida a la original. 5) ¿Qué realiza la transformada de Fourier? Toma señales seno idéales o combinación de esta misma en función del tiempo y posterior mente transfórmala al dominio de la frecuencia y viceversa. 6) ¿Qué es la transformada rápida de Fourier? Es un teorema matemático en el que se toma una frecuencia de muestreo o una frecuencia trasformada en base al tiempo denominada en muchos casos como “x(t)”, donde se busca como su nombre lo indica trasformar la señal.

Segunda parte. Ejercicio 4: Siendo 𝑥(𝑡) = 5s𝑒𝑛 (100𝜋 𝑡) + 6 𝑠𝑒𝑛 (250𝜋 𝑡) + 11 𝑐𝑜𝑠 (1100𝜋 𝑡) + 6 𝑠𝑒𝑛 (7000𝜋 𝑡) Resuelva: 4.1. Encuentre las frecuencias 𝑓0 de cada una de las componentes de la señal 𝑥(𝑡) Expresión general de una señal senoidal. f ( t )= Asin (wt ) Sabiendo que: w=2 πf

f 1=

100 Hz π =50 HZ 2π

f 1=

250 Hz π =125 HZ 2π

f 1=

1100 Hz π =550 HZ 2π

f 1=

7000 Hz π =3500 HZ 2π

4.2. ¿Se presenta fenómeno alias o aliasing si 𝑥(𝑡) es muestreada a 𝑆 = 1000 𝐻𝑧?? Explique paso a paso y si presenta alias, encuentre la frecuencia 𝑓𝑎 y reconstruya la señal 𝑥𝑎(𝑡) f s=1000 Hz Esta frecuencia genera aliasing en la 3 y 4, dado que no cumple con el teorema de Nyquist donde es: 1000 Hz ≤1100 Hz 1000 Hz ≤7000 Hz Observando esto podemos determinar que para que no se presente este problema, la “fs” debe de ser el doble o mas que la frecuencia mas alta de la seña. En este caso debemos tener el en cuenta el teorema y aplicamos la ecuación de frecuencia de alias. f a=f −Nfs Donde: “ f a” es la frecuencia numero uno de las dos que queremos reconstruir, “f ” es la frecuencia existente, “N” es el número de componentes con alias y “fs” es la frecuencia de muestreo dada. Remplazamos y resolvemos: f a 1=1100−( 1 ) 1000 f a 1=100 Hz f a 2=7000− ( 2 ) 1000 f a 2=5000 Hz Reconstrucción de la señal “𝑥𝑎(𝑡)”.

f a (t )=5 s en ( 100 π t ) +6 sen ( 250 π t ) +11cos ( 2 π ( 100 ) t ) +6 sen(2 π (5000)t ) 4.3. ¿Se presenta fenómeno alias o aliasing si 𝑥(𝑡) es muestreada a 𝑆 = 6600 𝐻𝑧?? Explique paso a paso y si presenta alias, encuentre la frecuencia 𝑓𝑎 y reconstruya la señal 𝑥𝑎(𝑡) En este punto tuvimos el mismo caso que lo anterior, pero basamos todo en la nueva frecuencia de muestreo. Analizamos y vemos que el único alias que vemos es la 4.

fs≤ 7000 frecuencia de alias. f a 1=7000− (1 ) 6600 f a 1=400 Hz Reconstrucción de la señal “𝑥𝑎(𝑡)”. f a (t )=5 s en ( 100 π t ) +6 sen ( 250 π t ) +11cos ( 1100 πt ) +6 sen (2 π (400) t)

4.4. Halle el ancho de banda de la señal 𝑥(𝑡) y el ancho de banda de las dos señales reconstruidas en 4.2 y 4.3. Tenemos que para hallar el ancho de banda simplemente se toma la frecuencia mas alta y se resta por la frecuencia más baja: Bw=f max −f min Para la señal x(t). Siendo 𝑥(𝑡) = 5s𝑒𝑛 (100𝜋 𝑡) + 6 𝑠𝑒𝑛 (250𝜋 𝑡) + 11 𝑐𝑜𝑠 (1100𝜋 𝑡) + 6 𝑠𝑒𝑛 (7000𝜋 𝑡) Tenemos como la frecuencia más alta 7000 Hz y más baja 100 Hz. Bw=7000−100=6900 Hz

Teniendo esto encuneta para las 2 más que nos piden solo se repite el proceso y se resuelve con la formula. Señal reconstruida 4.2. f a (t )=5 s en ( 100 π t ) +6 sen ( 250 π t ) +11cos ( 2 π ( 100 ) t ) +6 sen(2 π (5000)t ) Tenemos que: f max =2∗5000=10000 Hz f min =100 Hz Bw=10000−100=9 900 Hz Señal reconstruida 4.3. f a (t )=5 s en ( 100 π t ) +6 sen ( 250 π t ) +11cos ( 1100 πt ) +6 sen (2 π (400) t) f max =1100 Hz f min =100 Hz Bw=1 100−100=1000 Hz

4.5. Halle la frecuencia de muestreo para que la señal 𝑥(𝑡) no presente fenómeno de Alias. Teniendo en cuenta la teoría de Nyquist y subiendo que la frecuencia más alta de la señal es de 7000 Hz. f s=7000 x 2=14000 Hz=14 kHz

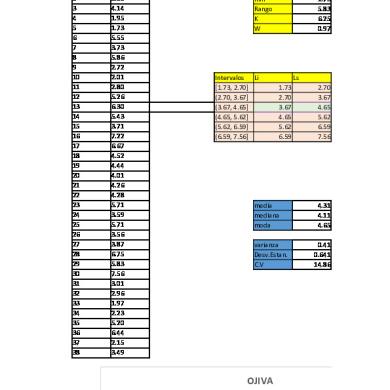
Ejercicio 5: Se va a muestrear una señal con niveles de amplitud entre -8V y 8V, y se va a cuantizar por redondeo con un error rms 𝜎 = 26 𝑚𝑉. Información para que se debe tener en cuenta. Rango dinámico o intervalo de escala. D=v−v−¿ D=8 v−(−8 v ) D=16 v Niveles de cuantización. L=2 dB Error rms. σ=

∆ √ 12

∆ “delta”; espacio entre niveles de cuantización. ∆=

D L

5.1. ¿Cuántos bits 𝐵 se requieren? Para este debemos utilizar la ecuación error rms y empezar a despejar dB. D ∆ L D σ= = = √12 √12 L √12 L=

D D =2dB= σ √ 12 σ √ 12

Para despejar 2dB debemos aplicar ley de logaritmos.

( σ √D12 ) D dB log 2=log ( σ √ 12 ) D log ( σ √ 12 ) dB= log 2dB=log

log2

Remplazamos y resolvemos. Dado que σ esta en mV, y D esta en voltios, debemos dejarlo en la misma unidad. σ =26 mV =0.026 v log dB=

( 0.02616√12 ) log 2

dB=7.47 dB 5.2. ¿Si el cuantizador ahora es de 12 bits, cuál sería su error rms 𝜎? Error rms. σ=

∆ √ 12

Hallamos delta. ∆=

D L

Niveles de cuantización. L=2 dB Resolvemos. L=212=4096 ∆=

16 =0.004 v=4 mv 4096

Error rms. σ=

4 =1.15 mv √12

Las señales 𝑥[𝑛] 𝑦 𝑥𝑞 [𝑛] 𝑠𝑜𝑛: 𝑥 [𝑛] = {7.0, −7.0,6.0, −6.0,5.0, −4.5,3.0, −2.1} 𝑥𝑞 [𝑛] = {6.7, −6.5,5.8, −5.7,4.7, −4.2,2.7, −2.4}

5.3. ¿Cuál es la señal de error 𝑒(𝑛)? Para esto restamos la señal de muestreo con la señal cuantizada. x ( n )−xq (n) X(n) Xq(n) e(n)

7 6.7 0.3

-7 -6.5 -0.5

6 5.8 0.2

-6 -5.7 -0.3

5 4.7 0.3

-4.5 -4.2 -0.3

e ( n )=[ 0.3 ,−0.5 ,0.2 ,−0.3 , 0.3 ,−0.3 , 5.7 , 0.3 ] 5.4. ¿Cuál es la potencia de la señal de ruido? Potencia de señal de ruido. Formula. N−1 1 P N = ∑ ( e2 (n) ) N n=0 Donde N es el número de muestras. 1 P N = ( ( 0.3 )2 + (−0.5 )2 + ( 0.2 )2 + (−0.3 )2 + ( 0.3 )2 + (−0.3 )2+ ( 5.7 )2+ ( 0.3 )2 ) 8 33.23 P N= =4.15375 8 5.5. ¿Cuál es la potencia de la señal muestreada? 1 ( ( 7 )2 + (−7 )2+ ( 6 )2+ (−6 )2 + ( 5 )2 +(−04.5 )2 + ( 3 )2 +(−2.1 )2 ) 8 228.66 P N= =28.5825 8 P x=

5.6. ¿Cuál es la relación señal ruido del cuantizador 𝑆𝑁𝑅𝑄? Paramero relación ruido. Formula. SNRQ dB=10 log

Px PN

Remplazamos y resolvemos.

3 2.7 5.7

-2.1 -2.4 0.3

SNRQ dB=10 log

28.5825 4.15375

SNRQ dB=8.3766 dB Sabiendo que de 12 dB hacia arriba es un buen cuantizador, sabiendo esto podemos concluir que este no es muy bueno.

Tercera parte. cada estudiante realizará el algoritmo de la Transformada Discreta de Fourier, en el cual debe estar planteada la sumatoria de la transformada con dos ciclos for. Dicho algoritmo se realizará para una señal de longitud de tres (3) muestras. Los tres valores de las muestras corresponden a los tres últimos números del documento de identificación, por ejemplo, si mi cédula es 80765437, entonces el algoritmo se hará para la señal x[n] = [4 3 7]. Para desarrollar esta parte el estudiante podrá utilizar Matlab, Octave Online, o Scilab. C.C. 1110589404 x ( n ) =[ 4 0 4 ]

Video: https://youtu.be/_exFHHPwABQ

Cuarta parte. cada estudiante investigará sobre el rango de frecuencias que el oído humano es capaz de escuchar, además investigará cual es el rango de frecuencias que emiten cinco (5) instrumentos musicales, se debe tener en cuenta los armónicos de los instrumentos ya que son las frecuencias más altas que emiten, y a partir de este dato, argumentará a que frecuencia de muestreo mínima se debe muestrear cada uno de los cinco (5) instrumentos musicales para ser digitalizados de manera correcta. Por ejemplo, si el bombo tiene un rango de 50 Hz a 15 KHz, Fs = 30 KHz mínimo. Frecuencia oído humano. en estándares normales el oído humano tiene un rango de 20 a 20000 Hz, siendo esto mismo los que capta sin generar incomodidad. Instrumento Platillos violonchelo Guitarra acústica Trompeta Piano

Frecuencia de muestreo mínima. Frecuencias (Max, min), Frecuencia de muestreo armónicos. mínima (Fs). 1 a 15 KHz 30 KHz 1 a 6.5 KHz 13 KHz 1 a15 KHz 30 KHz 1 a 7.5 KHz 15 KHz 5 a 8 KHz 16 KHz

Bibliografía. Información investigada. https://www.youtube.com/watch?v=9GxcNyGQsuk https://www.nobbot.com/educacion/que-es-la-transformada-de-fourier-y-para-que-sirve/ https://www.widex.cl/es-cl/blog/rango-auditivo-humano#:~:text=Mientras%20que %2020%20a%2020%2C000,a%20partir%20de%200%20dB. https://www.hispasonic.com/reportajes/tabla-rango-frecuencias-instrumentosmusicales/39