Tarea 4

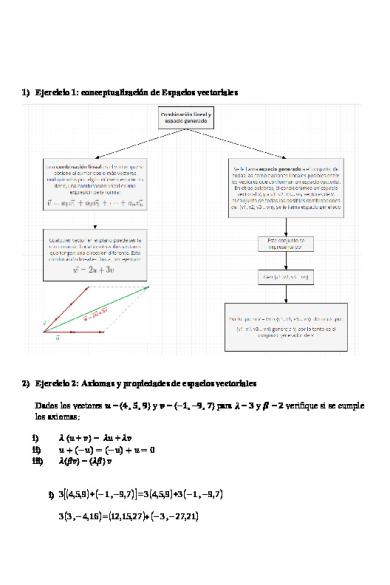
1) Ejercicio 1: conceptualización de Espacios vectoriales

2) Ejercicio 2: Axiomas y propiedades de espacios vectoriales Dados los vectores 𝒖 = (𝟒, 𝟓, 𝟗) y 𝒗 = (−𝟏, −𝟗, 𝟕) para 𝝀 = 𝟑 y 𝜷 = 𝟐 verifique si se cumple los axiomas: i) ii) iii)

𝜆 (𝑢 + 𝑣) = 𝜆𝑢 + 𝜆𝑣 𝑢 + (−𝑢) = (−𝑢) + 𝑢 = 0 𝜆(𝛽𝑣) = (𝜆𝛽) 𝑣

i) 3 [ ( 4,5,9 ) +(−1 ,−9,7) ] =3 ( 4,5,9 ) +3(−1 ,−9,7)

3(3 ,−4,16)= (12,15,27 )+(−3 ,−27,21)

( 9 ,−12, 48 )=( 9 ,−12,48 ) Si cumple el axioma

ii) ( 4,5,9 )+ (−4 ,−5 ,−9 )=(−4 ,−5 ,−9 ) + ( 4,5,9 )=0 (0,0,0)=(0,0,0)=0 Si cumple el axioma

iii)

3 ( 2 ⋅ (−1 ,−9,7 ) )=( 3⋅ 2)(−1 ,−9,7)

3 (−2 ,−18,14 )=6(−1 ,−9,7)

(−6 ,−54,42 )=(−6 ,−54,42) Si cumple el axioma

3. Ejercicio 3: Conjuntos generadores y Dependencia lineal. a. Determine si el conjunto 𝑆 es linealmente independiente 𝑆 = {(5,1), (−2,7), (3,2)} Se plantea la ecuación vectorial: c 1 (5,1 ) + c2 (−2,7 ) + c3 ( 3,2 )=(0,0) Nos daría el siguiente sistema de ecuaciones: 5 c1 + (−2c 2 ) +3 c 3=0 c 1+ 7 c 2+2 c 3=0

{

Resolvemos por el método gauss jordan:

(

5 −2 3 0 1 7 20

|)

1 F1→ F1 5

(

−2 5 1 7

3 0 5 0 2

F 2 → F 2−F 1

−2 5 37 5

3 50 70 5

F2→

1

−2 5

2 F 1 → F 2+ F 1 5

0

1

3 5 0 7 0 37

1

|)

( |) ( |) 1 0

5 F2 37

25 37 0 7 0 37

( |) 1 0 0 1

El conjunto S es linealmente dependiente b. Determine si el conjunto 𝑆 genera a ℝ3 𝑆 = {(2, −1,4) , (3,9,2) (4, −2,7)} Se plantea la ecuación vectorial: c 1 (2 ,−1,4 ) +c 2 ( 3,9,2 )+ c 3 ( 4 ,−2,7 )=( x , y , z )

( 2 c 1 ,−1 c1 , 4 c1 ) + ( 3 c2 , 9 c 2 , 2 c 2 ) + ( 4 c 3 ,−2 c3 , 7 c 3 )=( x , y , z) Nos daría el siguiente sistema de ecuaciones: 2 c 1+3 c 2 +4 c 3=x −c 1+ 9 c 2−2 c 3= y 4 c1 +2 c 2 +7 c 3=z

{

Resolvemos por el método gauss jordan: 2 3 4 x 1 −1 9 −2 y F 1 → F 1 2 4 2 7 z

|)

(

(

1

−1 4

3 x 2 2 2 F 2 → F 2+ F 1 9 −2 y 2 7 z

|)

3 2 21 2 2

( | ) ( | ) ( | ) 1 0 4

2

x x F 3 → F 3−4 F 1 2 0 2 y+ ¿ y 7

x 3 2 2 2 2 x F2→ F 2 0 1 0 y+ 21 2 0 −4 −1 z −2 x 1

x 3 2 2 2 x +2 y F 3 →−1 F 3−4 F 2 0 1 0 21 0 −4 −1 z−2 x 1

( ( ( (

1 0 0

1 0 0

1 0 0

1 0 0

3 2 1 0

x 2 2 x+2 y 0 21 1 8 x+ 4 y 2 x−z− 21

3 2 1 0

x 2 2 x +2 y F 1 → F 1−2 F 3 0 21 1 38 x −8 y−21 z 21

3 2 1 0

x 38 x−8 y −21 z −2 2 21 0 x +2 y 0 21 1 38 x −8 y−21 z 21

3 2 1 0

−131 x +32 y+ 84 z 42 0 x +2 y 3 F 1→ F 1− F 2 0 21 2 1 38 x−8 y −21 z 21

| ) | ) | ) | ) (

)

−131 x +32 y+ 84 z 3 x +2 y − 42 2 21 1 0 0 x+2 y 0 1 0 21 0 0 1 38 x−8 y−21 z 21

( |

((

))

)

−131 x +32 y+ 84 z 3 x +6 y − 42 42 1 0 0 x +2 y 0 1 0 21 0 0 1 38 x−8 y −21 z 21

( | ( |

−67 x+13 y + 42 z 21 1 0 0 x +2 y 0 1 0 21 0 0 1 38 x−8 y −21 z 21

)

)

El resultado es: c 1=

−67 x +13 y+ 42 z 21

c 2=

x+ 2 y 21

c 3=

38 x−8 y−21 z 21

Por lo que podemos decir que el conjunto S si genera a R3 4. Ejercicio 4: Determinantes, Rango de una matriz, e Independencia lineal Determinar el rango de la matriz A, por el método de determinantes y por el método de Gauss Jordan. En cada caso detallar los procedimientos realizados

Método de determinantes

Ya que 3x3 es el máximo tamaño de los determinantes que se pueden crear en base a esta matriz, podemos asegurar queRan( A)≤ 3, y como al menos 1 número de cada fila y columna de la matriz es diferente de cero decimos que Ran( A)≥ 1.

Tomamos una determinante 2x2 en base a la matriz:

|12 13|=|3−2|=1 El resultado es diferente de cero, lo que quiere decir que el rango de la matriz es al menos: Ran( A)≥ 2 Por último, para determinar si el rango de la matriz es 2 o 3 tomamos un determinante 3x3 en base en la matriz: 1 1 1 2 3 5 =[ ( 1 ⋅3⋅ 6 ) + ( 1⋅5 ⋅1 ) + ( 2 ⋅ (−1 ) ⋅1 ) ]−[ (1 ⋅3 ⋅1 ) + (−1⋅5 ⋅1 ) + ( 2 ⋅1⋅6 ) ] 1 −1 6

|

|

¿ 18+5−2−(3−5+12) ¿ 21−10 ¿ 11 El resultado es diferente de cero por lo que podemos asegurar que Ran ( A )=3 Método Gauss Jordan 1 1 1 2 A= 2 3 5 11 1 −1 6 29

(

)

1 1 1 2 A= 2 3 5 11 1 −1 6 29

)

1 1 1 2 A= 0 1 3 7 0 −2 5 27

)

(

(

1 1 1 2 A= 0 1 3 7 0 0 11 41

(

)

F 2 → F 2−2 F 1 F 3 → F 3−F 1

F 3 → F 3+2 F 2

F 1 → F 2−F 1

1 0 −2 −5 A= 0 1 3 7 0 0 11 41

(

1 0 −2 −5 0 1 3 7 A= 41 0 0 1 11

(

F3→

)

1 F3 11

F 1 → F 1+2 F 3

)

F 2 → F 2−3 F 3

27 11 −46 A= 0 1 0 11 41 0 0 1 11 1 0 0

( )

1 0 0 2.45 A= 0 1 0 −4.18 Ran( A)=3 0 0 1 3.73

(

)

Ya que en cada fila y columna hay al menos un número diferente de cero podemos asegurar que Ran( A)=3

5. Ejercicio 5: Demostraciones matemáticas a partir del uso de axiomas, propiedades y operaciones relacionadas con espacios vectoriales.

Sean 𝒖, 𝒗 y 𝒘 vectores en ℝ3. Demuestre que 𝒖 ∙ (𝒗 × 𝒘) = (𝒖 × 𝒗) ∙ 𝒘

(u1 , u2 , u3 )∙(( v1 , v 2 , v 3 )×(w 1 , w 2 , w 3))=((u1 , u2 ,u3 )×(v 1 , v 2 , v 3 )) ∙(w 1 , w 2 , w 3) Se resuelven los productos vectoriales:

(u1 , u2 , u3 )∙( v 2 w3−w2 v 3 ; v ₁ w ₃−w₁ v ₃ ; v ₁ w ₂−w ₁ v ₂)=(u2 v 3−v 2 u3 ; u1 v 3−v 1 u3 ; u1 v 2−v 1 u2 )∙( w1 , w2 Se aplica el producto punto: u1 ( v 2 w3 −w 2 v 3 ) +u 2 ( v 1 w3−w1 v 3 ) +u3 ( v 1 w2 −w1 v 2 ) =w1 ( u2 v 3−v 2 u3 ) + w2 ( u1 v 3−v 1 u3 ) + w3 (u1 v 2−v 1 u 2) u1 v 2 w3 −u1 w2 v 3 +u2 v 1 w3−u 2 w 1 v 3+u 3 v 1 w 2−u3 w1 v 2 =w1 u2 v 3−w1 v 2 u3 + w2 u 1 v 3−w 2 v1 u3 +w 3 u1 v 2 −w3 v Organizamos las expresiones:

u1 v 2 w3 −u1 v 3 w2 +u2 v 1 w3−u 2 v3 w 1+u 3 v 1 w 2−u3 v 2 w1 =u2 v 3 w1−u3 v 2 w 1+u 1 v 3 w 2−u3 v 1 w2 +u1 v 2 w3 −u2 v 1