1.b.Oscilații mecanice și oscilații electromagnetice - teorie (3)

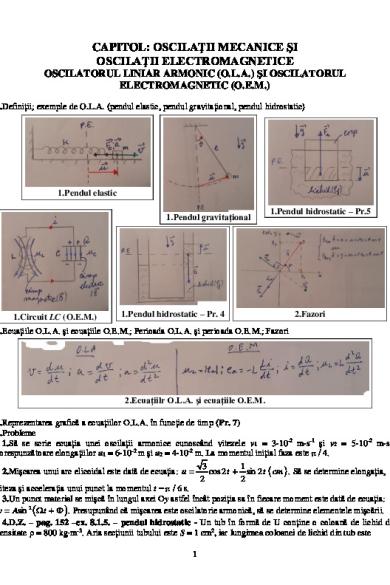
CAPITOL: OSCILAŢII MECANICE ŞI OSCILAŢII ELECTROMAGNETICE OSCILATORUL LINIAR ARMONIC (O.L.A.) ŞI OSCILATORUL ELECTROMAGNETIC (O.E.M.) 1.Definiţii; exemple de O.L.A. (pendul elastic, pendul gravitaţional, pendul hidrostatic)

1.Pendul elastic 1.Pendul gravitaţional

1.Circuit LC (O.E.M.)

1.Pendul hidrostatic – Pr.5

1.Pendul hidrostatic – Pr. 4

2.Fazori

2.Ecuaţiile O.L.A. şi ecuaţiile O.E.M.; Perioada O.L.A. şi perioada O.E.M.; Fazori

2.Ecuaţiilr O.L.A. şi ecuaţiile O.E.M. 3.Reprezentarea grafică a ecuaţiilor O.L.A. în funcţie de timp (Pr. 7) 4.Probleme 1.Să se scrie ecuaţia unei oscilaţii armonice cunoscând vitezele v1 = 3·10-2 m·s-1 şi v2 = 5·10-2 m·s-1 corespunzătoare elongaţiilor u1 = 6·10-2 m şi u2 = 4·10-2 m. La momentul iniţial faza este π / 4. 3 1 cos 2 t  sin 2 t  cm  . Să se determine elongaţia, 2.Mişcarea unui arc elicoidal este dată de ecuaţia: u  2 2 viteza şi acceleraţia unui punct la momentul t = π / 6 s. 3.Un punct material se mişcă în lungul axei Oy astfel încât poziţia sa în fiecare moment este dată de ecuaţia: y  Asin 2   t    . Presupunând că mişcarea este oscilatorie armonică, să se determine elementele mişcării. 4.D.Z. – pag. 152 –ex. 8.1.5. – pendul hidrostatic - Un tub în formă de U conţine o coloană de lichid de densitate  = 800 kgm-3. Aria secţiunii tubului este S = 1 cm2, iar lungimea coloanei de lichid din tub este 1

l = 0,5 m. Se produce o denivelare a lichidului din cele două ramuri având valoarea 2A = 8 cm. a) Să se arate că lăsând liber lichidul, acesta va oscila armonic (se neglijează frecările şi forţele de viscozitate). b) Să se calculeze perioada de oscilaţie a coloanei de lichid. 5.D.Z. – pag. 152 –ex. 8.1.4. – pendul hidrostatic - Un corp cilindric vertical de lungime l0 = 0,54 m, secţiune S = 5 cm2 şi densitate  = 800 kgm-3 este introdus în apă. Din poziţia de echilibru corpul este deplasat pe verticală în jos pe distanţa A = 2 cm. a)Să se arate că lăsând corpul liber, acesta va oscila armonic (se neglijează forţele de frecare cu aerul şi apa). b)Să se calculeze perioada de oscilaţie a corpului. c)Să se scrie legea de mişcare a corpului. 6.Un corp cu masa m = 0,01 kg, legat de un resort elastic orizontal, oscilează fără frecare, pe o masă orizontală, conform ecuaţiei: u  0,2 3 cos 2 t  sin 2 t  m  . Să se determine: a)pulsaţia, perioada, frecvenţa oscilaţiei precum şi faza oscilaţiei la momentul t = 0; b)momentele în care elongaţia este egală cu jumătate din amplitudinea oscilaţiei; c)ecuaţia vitezei şi ecuaţia acceleraţiei; d)momentele de timp pentru care viteza este 2 3 egală cu din viteza maximă; e)momentle de timp la care acceleraţia este egală cu din acceleraţia 2 2 maximă. 7.Un pendul elastic de masă m = 2∙10-2 kg efectuează o mişcare oscilatorie armonică, descrisă de ecuaţia:   u  5 sin  t   (cm). a)Precizaţi elementele oscilaţiei. b)Să se reprezinte grafic, în funcţie de timp: 3 6 elongaţia, viteza, acceleraţia şi forţa care acţionează asupra pendulului. 8.C.IX-X – pag. 73 – ex. 1.10.20. – Un oscilator liniar cu amplitudinea oscilaţiei de 8 cm se află, după 0,01 s de la începerea oscilaţiei, la distanţa de 4 mm faţă de poziţia de echilibru. Să se calculeze: a)pulsaţia oscilatorului; b)frecvenţa oscilaţiei; c)perioada oscilaţiei; d)viteza oscilatorului în poziţia dată; e)aceeleraţia oscilatorului în poziţia dată. 9.C.IX-X – pag. 74 – ex. 1.10.22. – Un oscilator constituit dintr-un punct material cu masa m = 1,6∙10-2 kg, atârnat la capătul unui resort, vibrează sub acţiunea forţei elastice a resortului, conform ecuaţiei:   u  101 sin  t   (m). Se cer: a)perioada şi frecvenţa oscilaţiei; b)viteza maximă şi acceleraţia maximă a 8 8 punctului material; c)valoarea maximă a forţei care acţionează asupra punctului material; d)timpul în care 3 punctul material efectuează drumul de la jumătatea amplitudinii la din amplitudine. 2 10.Legarea resorturilor - Două resorturi cu aceeaşi lungime în stare nedeformată, dar având constantele de elasticitate k1 şi k2 sunt legate de un bloc de masă m, pe o suprafaţă orizontală. Caculaţi raportul dintre perioada sistemului în cazul legării în serie a resorturilor (Ts) şi perioada sistemului când resorturile sunt legate în paralel (Tp).





Pr.12 – Condensatoare în serie

Pr.10 – Resorturi în paralel Pr. 10 – Resorturi în serie

2

Pr.12 – Condensatoare în paralel

11.Ce inductanţă trebuie să aibă un circuit oscilant care conţine un condensator cu capacitatea C = 2 µF, pentru a produce oscilaţii cu frecvenţa ν = 103 Hz? Se neglijează rezistenţa circuitului. 12.Legarea condensatoarelor - Se consideră circuitul oscilant din figura 1. Cum se modifică frecvenţa oscilaţiilor proprii şi de câte ori, dacă se schimbă comutatorul K din poziţia a în poziţia b? Se ştie că C2 = nC1. 5.Lucrare de laborator - Studiul pendulului elastic. Fig. 1

ENERGIA O.L.A. ŞI ENERGIA O.E.M. 1.Energia O.L.A. a.Energia cinetică (Ec) b.Energia potenţială elastică (Ep) c.Energia mecanică (Em) 2.Energia O.E.M. a.Energia magnetică (Wm) b.Energia potenţială electrică (We) c.Energia electromagnetică (Wem) Fig. 1 3.Reprezentări grafice a.Spectru energetic b.Schemă de nivele energetice c.Funcţie de timp: Ec = f (t); Ep = f (t); Em = f (t) d.Funcţie de elongaţie: Ec = f (u); Ep = f (u); Em = f (t) e.În spaţiul fazelor (u, p) 4.Probleme 1.Un bloc cu masa M = 3,62 kg este suspendat de un resort cu constanta de elasticitate k = 520 N·m-1. Un glonţ cu masa m = 4,5 g este tras de jos în sus cu o viteză v = 150 m·s-1 şi se opreşte în bloc. Aproximând mişcarea sistemului bloc-glonţ ca o mişcare oscilatorie armonică, să se afle amplitudinea mişcării. Problema 2

Fig. 2 Problema 1

Problema 3

2.Pe o scândură se află un corp cu masa m = 1 kg. Scândura efectuează oscilaţii armonice în plan vertical, cu perioada T = 0,5 s şi amplitudinea A = 2 cm. Se cer: a) Forţa de apăsare a corpului pe scândură şi valoarea maximă a acesteia. b) Ce amplitudine maximă A/ ar putea să aibă oscilaţiile pentru a nu se desprinde corpul de pe scândură ? c) Dacă scândura oscilează într-un plan orizontal cu perioada T/ = 5 s, corpul începe să alunece la o amplitudine A// = 0,6 m. Care este coeficientul de frecare dintre scândură şi corp? 3.D.Z. – pag. 154 –ex. 8.1.11. – Peste un disc de masă m1 = 0,8 kg este aşezat un corp de masă m2 = 0,2 kg. 3

Discul este legat de un resort (Fig. 1) a cărui constantă de elasticitate este k = 100 Nm-1. Între corpul de masă m1 şi suprafaţa orizontală nu se exercită forţe de frecare. Se imprimă sistemului viteza iniţială v0 = 0,2 ms-1. Să se calculeze: a) amplitudinea oscilaţiilor sistemului; b) valoarea minimă a coeficientului de frecare dintre corpurile de mase m1 şi m2 pentru ca m2 să nu alunece peste m1.   4.Un punct material de masă m = 2∙10-2 kg oscilează după legea: u  5 sin  15,6 t   (cm). a) Precizaţi 3  elementele oscilaţiei. b) Să se reprezinte grafic, în funcţie de timp, energia cinetică, energia potenţială şi energia totală. c) Să se determine momentele în care energiile cinetică şi potenţială sunt egale. d) Ce valoare are E A raportul c când u  ? e) Să se reprezinte grafic, în funcţie de elongaţia u, energia cinetică, energia 2 Ep potenţială şi energia totală. f) Să se reprezinte grafic, în spaţiul fazelor, „traiectoria” oscilatorului. 5.D.Z. – pag. 154 –ex. 8.1.13. – Două resorturi de constante k1 = 400 Nm-1 şi k2= 486 Nm-1 se află suspendate în plan vertical ca în figura 2.a. Resorturile se află în repaus, corpurile de mase m1 = 1 kg şi m2 = 1,5 kg aflându-se în plan vertical. Se deplasează corpurile pe distanţa A = 5 cm (fig. 2.b) şi se lasă libere. Să se afle:a) legile de mişcare ale celor două corpuri; b) intervalul de timp după care corpurile trec simultan prin punctul M, repetând mişcarea de la momentul iniţial; c) vitezele cu care corpurile trec prin poziţia de echilibru; d) raportul energiilor celor două corpuri. 6.În circuitul din figura 3 condensatorul cu capacitatea C este încărcat la tensiunea Um. Întâi se închide întrerupătorul K1. În momentul în care curentul prin bobina cu inductanţa L atinge valoarea maximă se închide întrerupătorul K2 şi se deschide întrerupătorul K1. Care este valoarea maximă a tensiunii la bornele rezistorului de rezistenţă R? 7.Un circuit oscilant este format din condensatoarele cu capacităţile C1 şi C2 şi o bobină de inductanţă L (Fig. 4). Ştiind că iniţial condensatorul C1 a fost încărcat la Fig. 3 tensiunea Um, iar condensatorul C2 a fost neîncărcat, determinaţi valoarea maximă a intensităţii curentului după închiderea întrerupătorului K. Se neglijează rezistenţa circuitului. 8.Care este valoarea sarcinii, raportată la sarcina maximă, de pe un condensator ce face parte dintr-un circuit oscilant LC, în momentul în care energia este egal repartizată între câmpurile electric şi magnetic? b) Care este intervalul de timp necesar pentru ca acest lucru să se producă, presupunând că la început condensatorul a fost încărcat cu sarcina qm? Se dau: L = 10 mH şi C = 1 µF. Fig. 4 9.După ce condensatorul unui circuit oscilant a fost încărcat cu sarcina electrică qm = 10-6 C, în circuit se produc oscilaţii electromagnetice amortizate. Ce căldură se degajă în circuit până când oscilaţiile se sting? Capacitatea condensatorului este C = 0,01 µF.

PENDULUL GRAVITAŢIONAL (P.G.) 1.Perioada P.G. 2.Probleme

Problema 1

1.Perioada P.G. 4

Problema 4

1.a)Care este expresia perioadei oscilaţiilor armonice ale unui pendul gravitaţional dacă acesta este suspendat de tavanul unui lift care urcă, respectiv coboară, cu o acceleraţie a (a  g) ? b) Dar dacă liftul descrie uniform, în plan orizontal, un cerc de rază R, cu viteza unghiulară  ? Se cunoaşte perioada T0 a oscilaţiilor armonice ale pendulului atunci când liftul este în repaus faţă de Pământ. 2.Care este expresia perioadei oscilaţiilor armonice ale unui pendul gravitaţional, dacă se ia în considerare forţa arhimedică? Se cunosc: T0 – perioada oscilaţiilor în vid,  - densitatea materialului din care este făcut pendulul, 0 – densitatea mediului în care oscilează pendulul ( 0  ). Se neglijează frecările. 3.Perioada oscilaţiilor armonice ale unui pendul gravitaţional la nivelul mării este T0 (raza Pământului fiind R0 şi acceleraţia gravitaţională g0). Care este expresia perioadei pendulului dacă acesta este ridicat la altitudinea h (h  R0), respectiv este coborât la adâncimea h ? 4.De tavanul unui vagonet este suspendat un pendul gravitaţional. Când vagonetul este în repaus pe o suprafaţă orizontală, pendulul oscilează armonic cu perioada T0. Ce expresie are perioada pendulului, dacă  vagonetul coboară liber, fără frecare, pe un plan înclinat de unghi  ?

COMPUNEREA OSCILAŢIILOR 1.Construcţia grafică a lui Fresnel 2.Probleme 1.Să se determine, în planul xOy, traiectoria mişcării unui punct material care este supus simultan oscilaţiilor: x  4sin  t  1 (cm) şi

  y  4sin   t   (cm). 2  2.C.IX-X – pag. 79 – ex. 1.10.64. – Un punct material execută o mişcare oscilatorie armonică datorită celor două oscilaţii care se 1  propagă pe aceeaşi direcţie şi au ecuaţiile: y1  4 sin 2   t   (cm) şi 3    y 2  3 sin  2  t   (cm). Să se scrie ecuaţia oscilaţiei rezultante. 2 

1.Construcţia lui Fresnel

TIPURI DE OSCILAŢII 1.Oscilaţii libere 2.Oscilaţii amortizate (Oscilator mecanic real şi Circuit oscilant real-Circuit RLC serie)

2.Oscilator mecanic real 2.Circuit RLC serie

3.Circuit RLC serie

5 3.Circuit RLC paralel

3.Rezonanţa elongaţiilor

3.Oscilaţii forţate - Rezonanţa

3.Rezonanţa tensiunilor

Bibliografie: 1.Manual clasa a XI-a (primit de la şcoală) 2.Manual clasa a IX-a ( înainte de 1989) – site: manualul.info (manuale din „Epoca de aur”) 3.Manual clasa a XI-a ( înainte de 1989) – site: manualul.info (manuale din „Epoca de aur”) 4.Compendiu de Fizică

6